⇒ Modeling the mechanical load effect on Ca2+ dynamics (…upcoming)
Your blood pressure changes almost from moment-to-moment depending on your posture (standing, lying), activity, and stress level. Your heart must continually adjust its force of contraction to compensate for the changing pressure. How does the heart do this? One way is via extrinsic signaling mechanisms involving baroreceptors in the blood vessels and neurohormones. The heart also has intrinsic mechanisms that enable the heart to adjust the force of contraction even without any neuronal input. The key questions we are addressing are: (1) What molecules are sensing the mechanical load on the heart? (2) What are the intracellular signals that carry the information about the mechanical load? (3) What molecules receive these signals and how do they respond? (4) How do these molecules, signals, and responses work together to regulate contractile force? We use mathematical modeling to answer this last question.
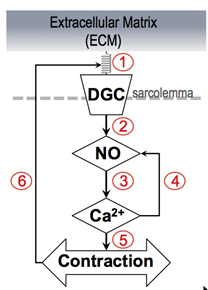
The mathematical model encapsulates the closed feedback loop shown in the figure. ① is the relative displacement between the extracellular matrix (ECM) or gel in our experiments and the mechanosensor (dystroglycan complex DGC) on the cell membrane. We hypothesize that a change in relative displacement alters the enzymatic properties of nitric oxide synthase (NOS) that changes the rate of nitric oxide (NO) production ②. NO and Ca2+ are reciprocally regulated (③ and ④) and changes in the Ca2+ concentration changes the magnitude of contraction ⑤. Closing the feedback loop ⑥, cell contraction alters the relative displacement between the ECM and the mechanosensor.
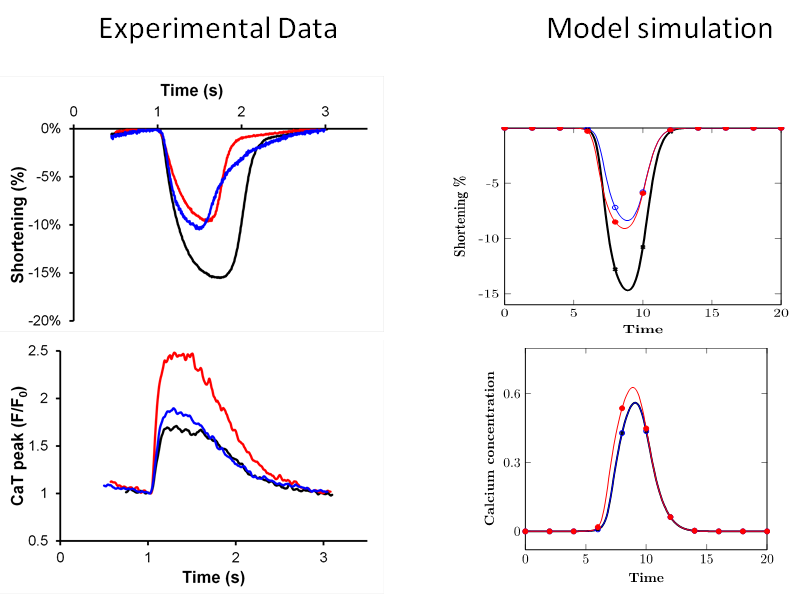The graphs below show experimentally measured contraction and Ca2+ transients with and without the gel to impose a mechanical load. The corresponding simulation results show that the model captures the qualitative features of experimental observations. Our work continues to bring the model to better quantitative agreement with the experimental data and, more importantly, identify conditions that lead to unstable dynamics. Identifying these conditions is important to understand how the interaction between the contractile system and the Ca2+ control system could give rise to load-dependent cardiac arrhythmias.
Your blood pressure changes almost from moment-to-moment depending on your posture (standing, lying), activity, and stress level. Your heart must continually adjust its force of contraction to compensate for the changing pressure. How does the heart do this? One way is via extrinsic signaling mechanisms involving baroreceptors in the blood vessels and neurohormones. The heart also has intrinsic mechanisms that enable the heart to adjust the force of contraction even without any neuronal input. The key questions we are addressing are: (1) What molecules are sensing the mechanical load on the heart? (2) What are the intracellular signals that carry the information about the mechanical load? (3) What molecules receive these signals and how do they respond? (4) How do these molecules, signals, and responses work together to regulate contractile force? We use mathematical modeling to answer this last question.The mathematical model encapsulates the closed feedback loop shown in the figure. ① is the relative displacement between the extracellular matrix (ECM) or gel in our experiments and the mechanosensor (dystroglycan complex DGC) on the cell membrane. We hypothesize that a change in relative displacement alters the enzymatic properties of nitric oxide synthase (NOS) that changes the rate of nitric oxide (NO) production ②. NO and Ca2+ are reciprocally regulated (③ and ④) and changes in the Ca2+ concentration changes the magnitude of contraction ⑤. Closing the feedback loop ⑥, cell contraction alters the relative displacement between the ECM and the mechanosensor.
The graphs below show experimentally measured contraction and Ca2+ transients with and without the gel to impose a mechanical load. The corresponding simulation results show that the model captures the qualitative features of experimental observations. Our work continues to bring the model to better quantitative agreement with the experimental data and, more importantly, identify conditions that lead to unstable dynamics. Identifying these conditions is important to understand how the interaction between the contractile system and the Ca2+ control system could give rise to load-dependent cardiac arrhythmias.